Chapters
This article provides you with a quick revision to normal distribution and continuous uniform distribution. In addition to this, it also offers a quick overview of when to use binomial versus Poisson distribution. At the end of the article, you will find a quick guide to approximations. So, let us get started with the normal distribution first.
Normal Distribution
- A method of modelling a characteristic among a population. For instance, the heights of people in London.
- You can use it to find out the probability of a specific trait or characteristic being observed. For instance, the likelihood of someone being up to 7 feet tall.
- It is bell-shaped because the likelihood of the value closer to the mean is greater. Similarly, it has less likelihood of containing an extreme value. For example, the majority of people are around 5-6ft tall, but very few are 4ft or 7ft.
- The probability of X is up to a specific value is taken as the area under the curve up to that point, and you can look up these values in the tables present in your formula booklet.
- To find the probability, you should standardize the score, using the following formula:
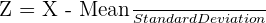
- The probability of an exact trait being observed is equal to zero due to the continuous scale. For example, the probability of someone being exactly 162.871cm tall is taken to be 0, because it is very unlikely.
- The total area under the curve is 1.
Important Properties of Normal Distribution
- The mean is represented by μ
- The variance is represented by
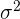. Remember that if you want to calculate the standard deviation, you should take the square root of the variance. - The mean, mode and median are equal in the normal distribution.
- The results of the normal distribution are interpreted as follows:
- Approximately 68% (two thirds) of the data values fall within
standard deviations of the mean (
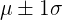) - Approximately 95% of the data fall within
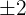standard deviations of the mean (
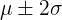) - Approximately all of the data, i.e. 99.7% falls within
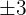standard deviations of the mean (
)
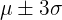- Approximately 68% (two thirds) of the data values fall within
Variables that can be modelled with a normal distribution
- We can model many real-life continuous variables by a normal distribution. However, to model those variables, the population should be sufficiently larger and the variable should be symmetrical with one mode
- X can have any real value for a normal distribution, but those values that are quite far away from the mean, i.e. more than 4 standard deviations away from the mean will have a practically zero probability density. This attribute allows us to model those variables that are not defined for all the real values. For instance, height and weight.
Variables that cannot be modelled with a normal distribution
- Variables containing more than one or no mode. For instance, the number generated randomly
- Variables that are unsymmetrical.
Standard Normal Distribution
- Because the normal distribution is symmetrical, hence with a standardized mean of 0: P(X< -1) is the same as P(X> 1)
Top tips for normal distribution problems:
1. Draw the distribution, label the mean, standard deviation and the X value interested in
2. Shade the area you need to calculate
3. Find the Z values you require (you may be taking one away from another, or taking one away from 1)
4. Look up the probability related to this value
5. Substitute these values into the equation you made depending on your shaded picture, and write out your full answer.
Continuous Uniform Distribution
- It is employed to model the probability of events occurring when there is a restricted range of possible outcomes, and it is equally likely for any of those values to take place.
- The expected value is E(X) and the variance is Var (X).
Binomial vs. Poisson
Binomial
- Use binomial, only if there is a number of trials given and two possible outcomes are being considered. In other words, the binomial distribution is used when the number of possible outcomes is only two, i.e. success or failure
- In binomial distribution mean is greater than the variance (Mean > Variance)
- The example includes tossing a coin as there will only be two outcomes (head or tail)
Poisson
- On the other hand, use Poisson, if there is an average or mean rate of something happening. In other words, there is no limit to possible outcomes in the Poisson distribution
- In Poisson distribution, the mean is equal to the variance (Mean = Variance)
- The example includes the number of spelling mistakes in an essay
Approximation
Normal Approximation of Binomial
- Use the normal approximation to binomial so X ~ B(n, p) becomes
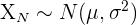, if n is large and/or if p is close to 0.5 - np > 5
- nq > 5, where 1 - p = q
- We can find out the mean and variance of a binomial distribution by using the formulae below:
Normal Approximation of Poisson
- Use normal approximation to Poisson so X ~ Po(L) becomes X ~ N(L,L), if L is large
- While doing this, you are required to use continuity correction because the probability of X being exactly equal to a value is zero for a normally distributed data. We can cover this next time, however, in the meantime, you can visit the link below:
https://revisionmaths.com/advanced-level-maths-revision/statistics/normal-approximations
Why do we use approximations?
If for a binomial distribution, there are a large number of values, then there can be many calculations involved. Consequently, it becomes inefficient to work with the binomial distribution. Nowadays, we can use calculators to calculate binomial probabilities, hence approximations are no longer required.
However, working with a normal distribution becomes easier because:
- We can quickly calculate the probability of a range of values
- We can employ an inverse normal distribution function (the majority of the calculators do not have an inverse binomial distribution function)
- In the exam, you are required to use the formula rather than the calculator to calculate the binomial probabilities. Hence, you are confined to small values of n.
Did you like this article? Rate it!
Loading...
Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian
I’m a junior high school,500 students were randomly selected.240 liked ice cream,200 liked milk tea and 180 liked both ice cream and milktea
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
Where is the answer??
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
ere is a 60% chance that a final years student would throw a party before leaving school ,taken over 50 student from a total of 150 .calculate for the mean and the variance
There are 4 white balls and 30 blue balls in the basket. If you draw 7 balls from the basket without replacement, what is the probability that exactly 4 of the balls are white?