Chapters
"The pure mathematician, like the musician, is a free creator of his world of ordered beauty."
-Bertrand Russell
Mathematics is an essential academic discipline that has many different topics worthy of studying such as geometry, trigonometry, and algebra.
Math is a subject that develops many of the key talents and skills that are highly desired by employers while also surfacing some priceless learnings along its course. Students will acquire critical thinking and problem-solving abilities that are important in a wide range of professions and areas of life.
Whether you need maths as a minimum entry requirement for your undergraduate course or could just use the extra points, I will walk you through what it is you need to do to get over the finish line and pass the final exam. The opportunities and doors that mathematics opens for students are endless.
It is also one of the more challenging subjects offered to students at school. Unfortunately for the majority of students who aren’t extremely gifted in the realm of mathematics, it is a core subject across secondary-level education meaning that it is compulsory for all students. Due to the subject being compulsory for all students, they may opt to study maths at a level which suits their ability.
In today's article, we will examine a lot of necessary information about algebra and try to encourage secondary school students to thoroughly enjoy their learning experience.
Check for a maths tutor near me here.

The Foundations of Algebra
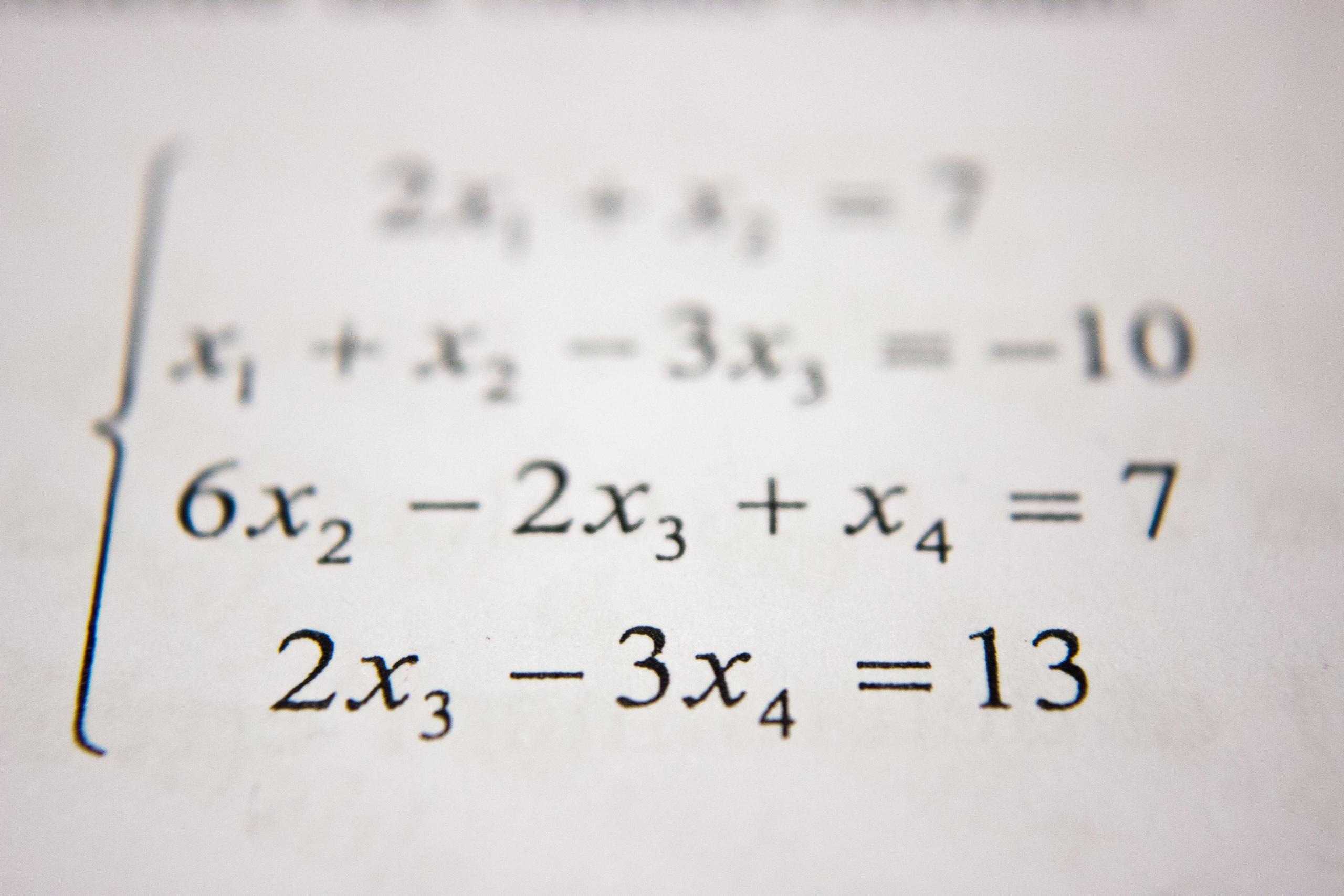
People's opinions about algebra are quite divided. On one side of the spectrum are those who greatly appreciate the logical expressions and efficiency of algebra, whereas, on the other hand, there are individuals who despise algebra's many rules and complexity.
Nevertheless, it is important to state that algebra is an essential academic discipline taught in schools worldwide; there isn't any way to escape so it's better to enjoy it thoroughly!
There are many branches of algebra one of them being linear algebra: linear equations that are about linear combinations. Linear algebra is used in almost all areas of mathematics that involve geometry, sciences, and engineering.
Since it is not uncommon to come across algebraic expressions that are extremely complex, algebra needs to be simplified to become more cognitive and straightforward.
How is it done?
Well, you might remember playing a game called “pass the parcel” as a kid which involved unwrapping a present layer by layer every time the music stopped. It’s one of those games kids play at parties, and can lead to tantrums…. But what has this got to do with algebra?
Imagine that the side of the equation containing the unknown (the letter) is a bit like that parcel. It has been wrapped in a set of layers one by one. The order that it was wrapped can be determined by BEDMAS or PEMDAS.
Algebra can be simplified by combining like terms, eliminating the parentheses, minus signs such as subtraction and negatives, and by following the BEDMAS or PEMDAS order of operations.
After discovering the origins and precise definitions of algebra, it is of the utmost importance to remember the benefits of studying algebra such as more efficient mathematics skills, improvement of logical thinking, and overall usefulness outside of school in daily life.
Find an online Maths tutor today on Superprof.
Where to Find an Algebra Tutor

After implementing many distinct techniques such as learning shortcuts, joining study groups, and asking your parents for your help, are you still struggling to grasp the essential concepts of algebra?
Have no fear, Superprof tutors are here to save the day!
Hiring a qualified tutor is the perfect solution to remedying any maths issues that you may face. Also, personal instructors specialising in any domain are highly recommended since they instil confidence in the student, provide personalised assistance, and are available at a time and place that best suits your needs.
When shopping around for a new algebra tutor, it is crucial to look for qualities that should be evident in the best academic instructors such as patience, communication skills, and teaching ability.
While there are many tutoring sites to consult on the internet available for citizens of the UK, the hands-down best option is Superprof.
With maths tutors offering sessions at competitive prices to improve algebra all over the United Kingdom, Superprof has a selection of tutors that will suit the needs of any person.
Hire a Superprof private educator today to remedy all your algebra woes; you won't regret it, we promise!
Search for many a maths tutor on Superprof UK.

Introduction to Variables in Algebra
Since algebra is such a layered academic discipline with many concepts, it is sometimes necessary to analyse each concept separately to acquire a further understanding of the entire subject.
What shall we examine now?
Variables. Becoming familiar with variables is necessary before solving, translating, or evaluating an algebraic expression; they are an essential aspect of algebra that cannot be ignored.
But what is a variable?
A variable can be defined as a letter that is used to replace a number. For example, the most commonly used variables that can be observed in algebraic expressions include the letters x, y, z, a, b, c, m, and n. Some letters such as i or e are not used as variables since they have other values in algebra. Also, it is important to mention that the letter o is never used since it might be mistaken for the number 0.
Considering the number of letters that potentially can be used as variables, there is one sign that should be avoided at all costs. Which is that? The multiplication symbol. The variable of x is used quite often for variables; therefore, using the multiplication sign could be an issue and cause unnecessary confusion for the student.
Variables are used to change verbal expressions into algebraic expressions.
Try your hand at practising some algebraic expressions and determining variables.
To learn more about variables and practise them, consult the Khan Academy Algebra I section to watch videos about examples containing one or multiple variables.
Discover different GCSE Maths tutor on Superprof.
Algebra Resources Online

Since we are living in the information or technology age, there is more information directly provided to us than ever before; long gone are the days of researching topics at the library!
Thanks to the developments of modern technology such as the internet, there are so many instructional sites worthy of consideration. Nevertheless, a wealth of information does not always mean that everything provided is trustworthy.
At times there seems to be more trash than treasure.
With that being said, it is important to consult reputable sources, like Superprof, as to which algebra websites are the most highly recommended. Without further ado, we will analyse the best websites and podcasts to learn more about algebra.
Reputable Algebra Websites
The following are the best online resources to learn more about algebra:
- Khan Academy: prides itself on offering free world-class education to all, Khan Academy is a fantastic and trustworthy site to consider the basic and more complex concepts of algebra. Some of the sections available for study on the Algebra I topic include algebra foundations, solving equations and inequalities, working with units, linear equations and graphs, and forms of linear equations.
- Mathplanet: although the study programmes offered on Mathplanet are intended for an American audience, the vital aspects of algebra that are examined are universal; that means even for UK students! Important categories include discovering expressions, equations, and functions, exploring real numbers, and how to solve linear equations. Also, each section includes theory, examples, and video lessons to improve comprehension of algebra.
The previously mentioned websites are brilliantly organised, engaging, and 100% trustworthy resources to learn more about algebra. After visiting these sites, you might not even need to look for anything more.
Discover different Maths tutor on Superprof.
Advice for algebra students
Students should start with the basics and work their way up, developing their skills by working through algebra questions and worked through solutions. It is important to trust the process, algebra is an extensive course and it is easy to get lost or bogged down in the sheer volume of material associated with it.
I encourage the students to wait until they are comfortable with the fundamentals of algebra before investing in extra books or courses. While these materials are frequently seen as an alluring shortcut to learning, it is crucial for students to understand that they are merely supplementary.
Before consulting any extra resources, you should first consult your basic algebra textbook to get the necessary background information in order to make the most out of your money and learning.
This textbook was specifically designed to include all pertinent information related to the course so you can be sure you won't miss any algebraic principles.
These books also adhere to a practical format that presents ideas before developing the corresponding theory and offering exercises so that students can hone their skills.
Learning algebra by using online resources has never been so much fun!
Basic Algebra Rules, Equations, and Examples
For each algebraic topic, you should have two to three worked-through examples in your notebook, followed by a sample exam question for that chapter.
Therefore, you have completed the essential materials, actively learnt by using examples to practice, and written down notes on the chapters for the leaving cert. I constantly emphasize to my pupils the value of studying for the exam as a whole rather than simply the subject that will be on it.
It's likely that not all of the algebra problems you've practised while going through the chapters won't be on your exam. Students will discover that each topic's exam questions often follow a specific format, therefore it's crucial to start getting practice answering exam-style questions.
Algebra, just like most things in today's society, is governed by rules and regulations. The rules experienced in algebra keep things organised and structured. There are various rules in algebra covering the topics of arithmetic, exponents, and radicals.
Algebra rules of arithmetic include the distributive property of multiplication and guidelines for adding, subtracting, multiplying, and dividing fractions among many others. The following list provides basic information about the previously mentioned algebra rules and how to obey them:
- Distributive Property of Multiplication: based on the fact that you're multiplying something by a sum of two or more distinct terms.
- Multiplying a Fraction: if you have the purpose of multiplying a fraction, times the numerator to achieve your goal.
- Dividing a Fraction: dividing a fraction is quite similar to that of multiplication except the denominator needs to be divided and then it will have the same effect as multiplying the numerator.
- Rules of Adding and Subtracting Fractions: the denominators must be identical and the numerators must be attached. Also, their sums must be placed over the common denominator.
Exponents are a quantity that represents the power to which a number or expression is to be raised, usually expressed as a raised symbol beside the name or phrase in algebra. The following are algebra rules for exponents:
- Zero-Exponent Rule: can be seen as a0 = 1 in equations and means that anything raised to the zero power is 1.
- Product Rule: the product of two powers with the same base is equal to the base raised to the sum of the two exponents. This rule can be effectively used by writing out the exponents as multiplications.
Another aspect that has a distinct set of rules is radicals.
What are radicals?
While there are many definitions for the word radical, in mathematics it means a quantity forming or expressed as the root of another. The following is an algebra rule for radicals:

The algebraic expression pictured above fits with the critical exponent rule of 
Before mentioning essential information about algebraic equations, it is important to define what an equation is: an equation can be understood as two expressions on either side of a sign that indicates their relationship. The relationship in an equation can have the same value, be less than, be greater than, or both.
Algebraic equations have terms and components that represent different things. For example, if a term includes letters and numbers, the messages are known as variables, and the numbers are the coefficients. Also, another rule of equations is that if the words have precisely the same variable, they become known as like terms and they can be added, subtracted, divided, and multiplied as if they were simple numbers.
Also, it is important to state that to solve equations at times the expression needs to be rearranged and the x needs to be isolated.
Many algebra examples can be found on reputable sources such as Study.com and Mathplanet.
In conclusion, by analysing many distinct aspects of algebra students become familiar with an important section of mathematics before, during, or after secondary school.
























