Chapters
Mark Maclaine explains how to understand BIDMAS to make answering those GCSE and Key Stage 3 Maths questions a lot easier.
‘Order of operations’ is just a way of saying: if a sum has a lot of ‘operations’ (multiply, add, subtract etc), which one do you do first? It might seem not to matter, but it makes a huge difference to the answer! In some countries like the UK this is called “BIDMAS” or “BODMAS” and in the US it is called “PEMDAS”.
If you do one thing today to prepare for your GCSE 9-1 level exam, allow reading this article to be it! Learning how to apply the BIDMAS rule in maths is a great return on investment when it comes to your study time.
Learning the Order of BIDMAS and subsequently practising applying the rule to several different equations will go a long way towards securing the grade you want in the subject.
Let's delve into this rule before looking at why you should spend time practising applying it.
You should take time and familiarise yourself with the different GCSE grade brackets.


What is the BIDMAS rule?
If you are a student preparing for the GCSE 9-1 maths exam then you will likely be able to remember at least a few times in the past when you fell victim to the tricky BIDMAS rule.
Often students can be certain that they have arrived at the correct answer in their maths homework or even in an exam setting only to find that they were not awarded full marks for their efforts. If you find that you were only awarded a low or mid partial credit for all of your hard work it is likely due to the order in which you carried out your calculations.
You mightn’t have even been aware of this, but the order in which you carry out your calculations can have a significant impact on the answer that you receive for the respective question.
So no matter how many times you punch the question into your calculator, your answer may keep appearing and your teacher will still tell you that you are incorrect, but why is this?
In maths we have a particular order that is provided to us in the BIDMAS acronym, it is also known as BODMAS, though regardless of which one of these you are thought at school they will provide you with the same answer.
The rule is in the BIDMAS acronym's alphabetical order, which stands for Brackets, Indices, Division, Multiplication, Multiplication by One, Addition, and Subtraction. According to the BIDMAS rule, multi-operator mathematical equations must be resolved in the BIDMAS order from left to right.
Similar to how Addition and Subtraction depend on which comes first in the respective maths problem, Division and Multiplication are also considered interchangeable operations. While the remaining elements, if mixed up will have a significant impact on the answer you receive.
An alternative acronym to BODMAS for remembering the sequence of events is the BIDMAS rule. The I in place of the O is the only distinction.
The implications are the same. The term "bidmas" is now more frequently used in primary schools. Brackets, Indices, Division/Multiplication, Addition/Subtraction are abbreviated as Bidmas.
Take your maths study home with you over the holidays with Christmas maths problems.
Again, Here’s what they stand for:
Brackets: (anything in brackets first)
Indices/Order: technical word for ‘powers and roots’ ie 32, √9 etc.
Division: ÷
Multiplication: ×
Addition: +
Subtraction: −
Note: In the US system the first two letters stand for Parentheses, their word for brackets, and Exponents, what they call powers.
With maths, it is always easier to practice something if you fully understand the principle. This is often best achieved through using short stories to add context to what you are doing in mathematical terms.
It is important that we translate even more complex equations into simple English terms in order to arrive at a comprehensive understanding.
One useful way of teaching this involves the following story. Imagine a market trader selling some cheap fruit. He sells 4 apples costing 5p each and an orange costing 10p. The buyer doesn’t have any money so the seller agrees to write it down.
4 × 5 + 10
The buyer thinks to himself: “That’s 4x5, which is 20p, then plus 10.”
The buyer comes back the next day and wants to pay. He brings 30p with him. However, the shopkeeper says “No! That’s not it. Look:” he shows the man his notebook:
4 × 5 + 10
"See it’s 5+10, which is 15p, and then you multiply by 4. That’s 60p!" He says.
The buyer gets very annoyed. Now, who is right? If you’re reading this as a Maths tutor, why not ask your students to imagine they are the shopkeeper, or the buyer, and argue for the order they think is right?
Without knowing the order of operations, either of them could be right. If we know to do multiplication and division before doing any addition and subtraction, we can see that the buyer must be right: 4x5p gives you the cost of the apples (20p), and then adding 10p for the orange gives the total (30p).
Now imagine a different buyer buying one apple and one orange every day. She goes on holiday for four days and wants to buy fruit to last for her holiday. Now, what should the sum be? Since an apple is 5p and an orange is 10p, we could still write the sum:
4 × 5 + 10
But this time, we need to do 5+10 for an orange and an apple, and then multiply that by 4, for the four days. So we add brackets.
4 × (5 + 10)
Now we can see that we need to do 5p+10p, which is 15p, and then multiply by 4 to make 60p.
Understanding BIDMAS, or the order of operations, is key to many areas of maths, including algebraic problems. See my post next week to see how to put it into practice.
If you need some help with maths, why not look at the Superprof website and find Maths Tutors in your area?
Why it is important to learn BIDMAS
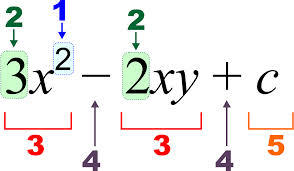
If you are still wondering why you should spend your valuable time learning how to apply the rule then you should consider a few things. First and foremost it is purely a matter of how we choose to define the notation. The main reason for it is that it lets us write polynomial expressions without parentheses.
If you are struggling to learn BIDMAS then why not consider working with a private maths tutor to help grow your confidence in maths?
e.g., ?3+3?2?−41?+2?x3+3x2y−41x+2z
These equations frequently appear in the GCSE exams across all levels. While BIDMAS will never be specifically examined in your exam paper. You will need to depend on the rule indirectly a lot over the course of your exam.
However, rather than trying to strictly follow one style or the other, what counts is that the notation is clear and unambiguous, therefore statements like a/bca/bc should be avoided (and replaced with something like abcabc depending on what is intended).
It would be fundamentally incorrect to attempt to "prove" a notational convention or to view it as anything other than a method that has been agreed upon to effectively transmit meaning.
Having a strong grasp of how to apply BIDMAS when you are going about solving an equation will result in you achieving a high part in the respective question.
While you will of course be awarded a partial credit if you happen to confuse the order in which you solve an equation such as the problem above, Losing out on these marks over the course of your entire exam will certainly add up. It can often be the difference in students falling down a grade bracket on the day.
So this is perhaps the greatest incentive for students to familiarise themselves with the BIDMAS rule sooner rather than later as it will likely result in you attaining a higher result in the final exam.
Another reason for students to improve their ability to apply the BIDMAS tule is that it is transferable across to a variety of different chapters in the GCSE 9-1 maths syllabus.
This means that you will be rewarded for the time that you spend studying as you will be able to apply your learnings across an array of different mathematical topics and improve your overall understanding of the subject.
The new maths 9-1 GCSE can be confusing if you don’t know what grade is what.

Practice BIDMAS or BODMAS with a tutor
There is always space for progress, whether you are at the top of your class or find it difficult to keep up with the pace set by your GCSE math teacher!
You might find yourself working against the clock to completely cover the information during the GCSE 9-1 level exams. Students may be forced to juggle multiple studies at once as a result, which is undoubtedly stressful in situations like these.
Students can find qualified tutors for their particular subject on the website Superprof. Students can choose from a wide variety of tutors here with a variety of backgrounds. Students are then able to choose tutors based on their specific needs, budget, and vicinity.
Additionally, the service gives students some latitude in how they approach their math studies. The majority of instructors who advertise their services on the platform offer in-person, at-home, and online learning choices.
If you're still not sure, the first class is frequently free, giving students who might still be on the fence the option to try out the program before committing.
If you could just avoid all of the trial and error processes with your studies, you could save a significant amount of time. If you've taken your GCSEs previously, you know that time is never in abundant supply while you're studying the subject. It can take pupils months to determine what learning method suits them.
With Superprof, you can be sure to discover the ideal tutor to guide you along the path, whether you are studying for a test, need assistance with your homework, are learning the fundamentals or are tackling more difficult topics.
You might be able to do it with the aid of a math tutor. Professional math tutors frequently have years of experience working with GCSE students, assisting them in realizing their potential in the subject.
This indicates that they will be familiar with the most effective study methods and exam strategies, saving you the time and effort of having to figure it out on your own.
At Superprof, the ideal tutor for your learning style may be just around the corner. So why are you still waiting? Today, take the first step in expanding your math skills.